Graph Drawing Challenge (Upward Crossing Reduction)
Who has the best Sugiyama style layout?
As with last year's contest, we shall hold the Graph Drawing Challenge
in a format similar to a typical programming contest. At the start of
the challenge, teams of contestants will receive the collection of
challenge-graphs. After one hour, the teams will submit their final
drawings and the team with the highest cumulative score wins.
Teams will be allowed to use any combination of software and human
interaction systems to produce the best drawings. To accommodate both
teams wishing to prepare for the challenge and teams wishing simply to
participate, with no preparation, we will be providing, in advance, a
small set of graph visualization tools. These tools are not
necessarily meant to solve the problems at hand but are there to help
the teams manually draw and manipulate the graphs. To further
the development of new tools and to help promote tools already in
existence, teams are also welcome and highly encouraged to create and
bring their own software packages.
There exist two categories in the challenge that are judged differently:
- Automatic -
This category is for teams using their own tool.
Since we assume that the tool contains special algorithms to solve
the challenge automatically, these teams will receive larger
challenge graphs. Manual fine-tuning is allowed.
- Manual -
This category is for teams using the provided graph editor.
The graph editor does not contain any specific algorithm to solve
the challenge. It allows only to move nodes and to re-route edges.
This category is for creating manual solutions without help of
an automatic algorithm. Teams in this category will receive smaller
challenge graphs.
This year the challenge focuses on minimizing the number of crossings
of upward grid drawings of graphs with edge bends.
The challenge graphs will be directed, acyclic and non-planar.
Multiple edges between the same pair of nodes may occur.
In particular, all drawings must have the following properties:
-
All nodes are placed on distinct integer grid locations.
-
Edges can have bends. All bends are placed on distinct integer grid locations.
-
Edges start at the source node and end at the target node.
Due to the bends, they form a path of edge segments from the source to
the target node.
-
All edge segments
must be upward; i.e., the start point of the segment must have a
strictly smaller y-coordinate than the end point of
the segment. There is no restriction on the x-coordinate.
-
Node and edge overlaps are forbidden.
-
Use the smallest number of edge crossings.
The results are judged solely with respect to the number of edge crossings.
Other aesthetic criteria such as symmetry of the placement or use of
area are not taken into account.
This allows an objective way to qualitatively evaluate a given drawing.
With this challenge, we hope to attract (not exclusively) all teams that
have developed an automatic
Sugiyama-style layout or any alternative
approach for directed acyclic graphs.
Here are some examples of allowed and forbidden situations.
For the challenge, it does not matter whether the y-axis is oriented
in mathematical convention with increasing coordinates towards the top,
or in English reading direction with increasing coordinates towards the bottom,
but in the drawings below, the origin (0,0) is near the bottom left corner,
that is, the y-axis is drawn in mathematical convention.
|
|
|
|
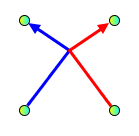
|
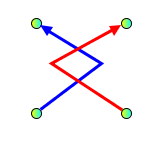
Allowed:
2 crossings
|
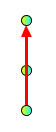
Forbidden:
Node overlaps edge
|
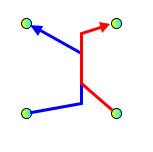
Forbidden:
Edge segments overlap
|
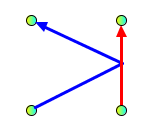
Forbidden:
Edge bend on other segment
|
Forbidden:
Knockknee (bends on same location)
|
Here is an overview of the rules for the challenge:
-
The challenge will take place for one hour during the Graph Drawing Symposium.
-
Teams may consist of one to three participants each.
Each team may bring their own computers and/or software tools to the challenge.
-
Software tools for manually solving the challenge
will be provided for each team with time available prior to the
challenge to set-up and practice with the system.
-
At the start of the challenge, contestants will receive a
collection of five to ten graphs.
The graphs will be directed acyclic non-planar with
twenty to five thousand nodes.
-
For each graph, the team submitting the drawing
with the smallest number of crossings receives the highest score. Scores for
other submissions of the same graph shall be weighed with respect to
this value.
The team with the highest total score over all graphs wins.
Remote Participation
For those teams that cannot attend the conference but still wish to
compete (in the automatic category), we allow remote participation.
A few key points:
-
Participants should contact the committee prior to the contest, and
preferably as early as possible, to help determine the number
of remote teams and to coordinate the instructions.
-
At the time of the challenge, remote teams will be able to access
an online location (website) to download the data sets and then
simply submit the results via email.
-
Detailed submission instructions will be provided on this site
at a later time.
Graph Format
For the GD2008 contest,
a modified ASCII format described below will be used.
The contest graphs will be provided in this format and
the final submissions should be prepared using the same format.
-
The first number (N) indicates the number of nodes in the graph.
-
The next 2N numbers contain the coordinates of the nodes.
Each coordinate consists of the x and the y value of the node,
indicating its position.
-
The remainder of the file contains the edges.
For each edge, the first value is the index of the source node, and
the second value is the index of the target node.
Next follows an array with an even number of values, enclosed by
[ ... ], which are the x and y coordinates
of the bend points of the edge.
-
An edge that has no bend points is written as an empty
bend array
[].
-
The nodes are labeled from 0 to N-1 and
the order from the input file must be used in the output file as well.
-
Comments are allowed as indicated below.
-
The edge order is not important.
-
The contest graphs will have random start locations for the nodes.
-
All numbers are integers.
Sample File
Below is a simple example:
# Lines starting with # are comments and ignored
# First value is NumNodes(N)
5
#
# Next N pairs are x and y coordinate values of each node
10 0 # Node 0
5 5 # Node 1
0 10 # Node 2
0 8 # Node 3
10 2 # Node 4
#
# Remaining lines are the edges.
# The first value is the source node.
# The second value is the target node.
# The values between [ ... ] are grouped in pairs as bend points (X,Y)
0 2 [ 9 5 5 9 ] # Edge from Node 0 to Node 2 with bend points (9,5) and (5,9)
0 4 [] # Edge from Node 0 to Node 4 with no bend points
0 1 [] # Edge from Node 0 to Node 1 with no bend points
0 3 [ 0 1 ] # Edge from Node 0 to Node 3 with bend point (0,1)
4 1 [] # Edge from Node 4 to Node 1 with no bend points
4 3 [ 5 4 ] # Edge from Node 4 to Node 3 with bend point (5,4)
4 2 [ 10 9 ] # Edge from Node 4 to Node 2 with bend point (10,9)
1 3 [] # Edge from Node 1 to Node 3 with no bend points
1 2 [] # Edge from Node 1 to Node 2 with no bend points
3 2 [] # Edge from Node 3 to Node 2 with no bend points
|
The diagram below corresponds to this input file.
It displays the K5 in a legal upward layout,
however the number of crossings in this layout is not optimal.
In this picture, the origin (0, 0) is near the
top left corner (English reading direction).
If your software has the origin at the bottom left corner
(mathematical convention),
your image will be mirrored in y direction.
Legal notice







