We have two creative topics that are judged independently:
- Game of Thrones: This graph models the relations between characters from the HBO series "Game of Thrones" by season 8.
- Mathematics Genealogy Project: This graph models supervisor/student relations between mathematicians.
Participants may submit drawings of both graphs (or only one graph).
Game of Thrones
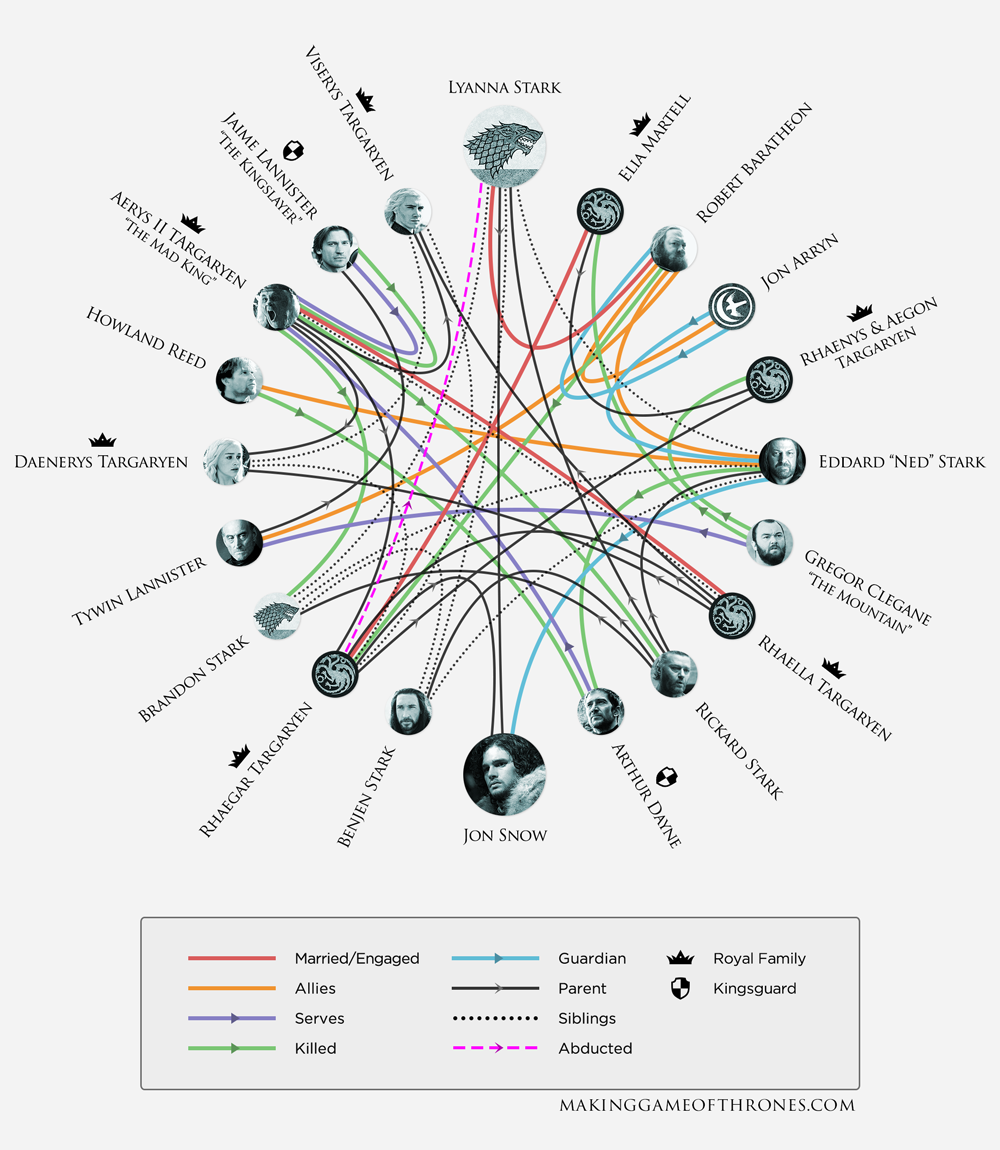
The TV show "Game of Thrones" is based on the book series "A Song of Ice and Fire" by George R. R. Martin and is one of the most popular TV shows in the previous years. In 2016, HBO released the following infographic that shows how the key players related to each other during the "Tower of Joy" moment.
This graphic inspired us to create a contest topic for Game of Thrones character relations. We extracted the relations between the most important characters in the show as of the end of Season 7 from the Game of Thrones Wiki. The graph consists of 84 nodes (characters) and 216 edges (relations).
The graph is provided in GraphML format. The nodes have the following properties. The optional properties do not have to be visualized, but can be.
| name | The name of the character. |
| status | Alive or Deceased. |
| house-birth | (Optional) Affiliation of the character to a house by birth. |
| house-marriage | (Optional) Affiliation of the character to a house by marriage. |
| group | (Optional) Affiliation of the character to a group that is not a house. |
The type of the relations are described by the relation property of the edges. The edges are directed if unspecified, or undirected of directed="false". There are the following types of relations.
| death | Directed edge: The source character killed the target character. |
| father | Directed edge: The source character is the father of the target character. The type property describes whether it's biological or legal. |
| mother | Directed edge: The source character is the mother of the target character. The type property describes whether it's biological or legal. |
| siblings | Undirected edge: The two characters are siblings. The type property describes whether it's biological or legal. |
| lover | Undirected edge: The two characters are lovers. |
| spouse | Undirected edge: The two characters are (or have been) married. |
| allegiance | Directed edge: The source character is allegiant to the target character. The type property describes the type of allegiance. |
The graph is available here.
Mathematics Genealogy Project
The Mathematics Genealogy Project is an initiative of North Dakota State University to track all advisor-advisee relationsships in the broader field of mathematics, since the earliest records that are available. The database has 222,360 scientists on record as of today, and can be explored here.
In July 2016, Cosmin Ionita and Pat Quillen of MathWorks used MATLAB to analyze the Math Genealogy Project graph. At the time, the genealogy graph contained 200,037 vertices. There were 7639 (3.8%) isolated vertices and 1962 components of size two (advisor-advisee pairs where we have no information about the advisor). The largest component of the genealogy graph contained 180,094 vertices, accounting for 90% of all vertices in the graph. The main component has 7323 root vertices (individuals with no advisor) and 137,155 leaves (mathematicians with no students), accounting for 76.2% of the vertices in this component. The next largest component sizes were 81, 50, 47, 34, 34, 33, 31, 31, and 30. The graph does contain cycles, but is generally very tree-like.
For the contest, we have selected the subgraph containing only the 2277 scientists who graduated before the year 1900, but retaining the number of descendants in the full graph. We also kept the year and country of each graduation. You task is to use this information to give the most meaningful or insightful visualisation of the graph. You may choose to leave out or emphasise information as you see fit.
The graph is provided as a simple text file. The file starts with a single line stating the number of vertices (2277), followed by 2277 lines describing the vertices, then a single line stating the number of edges (2554), followed by 2554 lines describing the edges. A vertex line contains the following space-separated fields:
| id | A unique integer id for the vertex. This is the original scientist id from the Mathematics Genealogy Project; since this is a subgraph, the integers are not consecutive. |
| descendants | The total number of the vertex descendants in the full graph. |
| name | The name of the scientist. The name may contain additional spaces, and may contain UTF-8 characters. |
| advisor | The id of the advisor. |
| advisee | The id of the advisee. |
| year | The year in which the graduation of the advisee took place. |
| country | The country in which the graduation took place. In some cases, country information is missing. |
The graph is available here.
Evaluation
For the creative topics, you are completely free to use any drawing style you wish. Your submissions will be judged both on aesthetic value and on the clarity of information displayed.
Submission
Electronic submissions (by email) must be received by September 15 (23:59 PDT) and must include the following information:
- Names and email addresses of the contributors.
- A visualization illustrating the graph in a format of your choosing.
- A brief description on how the graph and layout were produced.
- A web-friendly image of your visualization. Max resolution 1000 by 1000 pixels.
- A pdf version of your visualization, suitable for printing on a large A0 poster.
If your drawing requires special printing because of size, resolution, or color constraints, you are encouraged to submit via hard-copy. In this case, please contact us in advance and make sure that your submission is received no later than September 15. Please still submit the remaining items by email.
Please send your contest submissions to:
Maarten Löffler
PO Box 80.089
3508 TB Utrecht
The Netherlands